Discovering Data Structures – Binary Tree Traversal

In our last couple of posts, we talked about two things: the implementation of binary trees and recursion. First, we know that binary trees consist of a root node, that points to its own children, which then points to its own subsequent children. Second, we know that recursion is the process in which a function calls itself directly or indirectly. With these two big ideas in mind, we come to my last post about binary trees: traversal.

Common approaches to similar problems

There are a lot of coding problems that you may encounter that will have you traverse a tree to figure out a certain issue: searching an element within an unordered tree, finding the max height or depth of a tree, or making a deep copy of an object. The sky is the limit here, and likewise, there are tons of ways out in the wild to figure out these issues. Should we check the bottom nodes first? What order? Should we do it level by level?

What we’re going to do is focus on a few common approaches. We’ll talk about…

• Breadth-first search
• Depth-first search

Here’s an image from basecs (remember to cite your source) that breaks it down:

As the image above shows, DFS checks by subtrees. BFS checks by node level. For DFS in particular, we’ll go over PreOrder traversal, PostOrder traversal, and then inOrder traversal.

Breadth-first search traversal

Breadth-first search, or BFS, is the traversal method where we want to look at every single sibling on a given level before we move down the next level. So if you took a look at the last picture, it’s looking at all the reds, then the greens, then the blues. It’s looking horizontally.

Pseudocode

1. Create a queue (like an array)
2. Place the root node in the queue
3. Loop as long as there’s anything in the queue
   1. If there is a left child on the current node in the queue, add it to the queue
   2. If there is a right child on the current node, add it to the queue
   3. Remove the current node from the queue
4. Return variable that stores the values.

Keep in mind this is a very basic implementation. Maybe you want to keep track of all the nodes that you visited already, which may mean you need another data structure to keep track of that instead of just throwing it out altogether.

Reasons for the queue

The reason why you need the queue is that since sibling nodes aren’t directly linked together, you need some sort of separate structure to keep track of all the nodes you visited already, hence the need for a queue.

Also remember, queues have that FIFO (first in, first out)characteristic, meaning the first element is always being shifted out after it’s visited, and subsequent child nodes will be pushed to the end of the line, eventually making its way to the front of the line so it’ll be checked. The drawing from the same blog post helps visualize what I’m talking about.

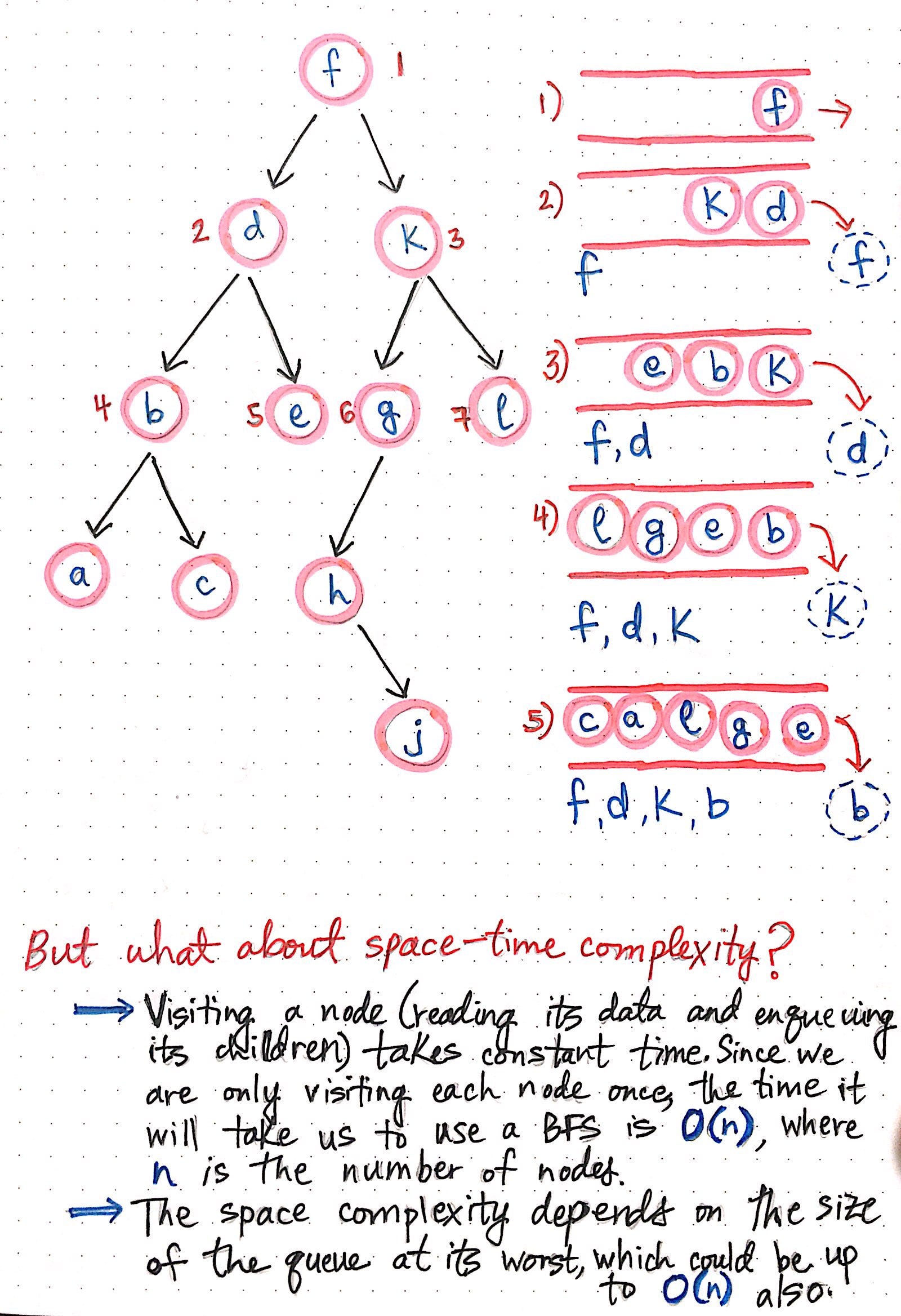
Implementation

function bfs(rootNode){
  //check to see if root node exists
  if(rootNode === null){
    return; 
  }

  //create queue, push root node into it 
  let queue = []
  queue.push(rootNode)
  
  //continue to traverse through queue as long as it's not empty
  while(queue.length > 0){
    //ref to current node, which is first element in queue
    let currentNode = queue[0]

    /*
      This may be a good spot to place some other implementation, like logging the value of a node to the console. It all really depends on the problem you're trying to solve
    */

    //if currentNode has left or right child nodes, add them to the queue
    if(currentNode.left !== null){
      queue.push(currentNode.left)
    }

    if(currentNode.right !== null){
      queue.push(currentNode.right)
    }

    //remove currentNode from queue
    queue.shift()
  }

}

Depth-first search traversal

“Wait a minute, I thought you said you were going to talk about recursion in this post.” Well, now that we moved passed BFS, we’re going to go into DFS, which definitely uses recursion.

Like in the image way earlier in this post describes, DFS traverses by going through the left subtrees first, and then the right subtrees, rather than like in BFS, go level by level. Like it’s namesake, we go depth-first, or vertically.

In this post, we’ll go through three variants:

• PreOrder traversal
• PostOrder traversal
• InOrder traversal

Changing the order of the lines of codes within our DFS function(s) dictates which type of DFS traversal method we end up using. GeeksforGeeks has a nice post that gives comparisons and examples of what each of these three will look like. Leetcode also has a section to go over Binary Trees and has some problems to write code for each. We’ll go over them briefly.

PreOrder Traversal

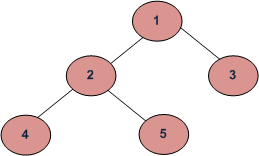
Given the above image, Preorder exploration would go in this order:

(Root, Left, Right) : 1 2 4 5 3

Pseudocode and implementation

Let’s say you want to output the order in which the tree gets traversed. You could do the following:

1. Create an array to hold all the node values
2. Create a helper function that accepts a node
   1. If the node is not null
      1. Push the result to the array
      2. Call the helper function for the left side of the tree
      3. Call the helper function for the right side of the tree
3. Call the helper function and pass the root node as its argument
4. Return the result

var preorderTraversal = function(root) {
    let result = []
    preorder(root)
    
    function preorder(root){
        if(root){
            result.push(root.val)
            preorder(root.left)
            preorder(root.right)
        }
        
    }
    return result
};

See the recursion in action? The function preorder is calling itself within the function body. Remember the idea of the call stack and the ‘unwinding’ execution order of a recursive function. Let’s say in the above example with the numbers, we start with the root node with a value of 1, push the value to the array, and then call the preorder function with the left child of the root. The function call to the right node will be called later. The process starts all over again by pushing 2, check its own left child, and adding 4. With no more leftward nodes, it’ll start to backpedal by checking the right child node of 2, which is 5, add that value to the array, go unwind again, and then go back to our original calls to the root node, finishing off with checking the right side of our tree. I hope you can visualize it through these words! It can get pretty difficult.

If you can get this, then you can get PostOrder and InOrder traversal.

PostOrder Traversal

Given the above numerical example, postorder traversal would look something like this:

(Left, Right, Root) : 4 5 2 3 1

Implementation

var postorderTraversal = function(root) {
    let result = []
    poTraversal(root)
    
    function poTraversal(node){
        if(node){
            poTraversal(node.left)
            poTraversal(node.right)
            result.push(node.val)
        }
    }
    return result
};

Notice how the function is more or less similar to the PreOrder implementation, but the order of the lines within the helper function is different. Instead of checking the root first, we travel all the way down to the leftward most child, then the right, and push our values, and then push the root.

InOrder Traversal

Finally, given our example, InOrder would go in this order:

(Left, Root, Right) : 4 2 5 1 3

Implementation

var inorderTraversal = function(root) {
    let result = []
    recurInOrder(root)
    
    function recurInOrder(node){
        if(node){
            recurInOrder(node.left)
            result.push(node.val)
            recurInOrder(node.right)
            
        }
    }
    return result
    
};

Again, it’s a subtle change, but we look at the left first, then the root node, and then the right.

Remember, a change in a single line of code can lead to widely different results.

Conclusion

Phew! That’s a lot to digest. It was definitely a lot to take in for me when I was first tackling this subject. Take the time to read this post and all the other things I linked to and then when you’re ready, do some practice problems to test your ability and knowledge of the problem.

Good luck!