Discovering Data Structures – Binary Tree Implementation

In my last post, we talked about the binary search tree, what it is, and it’s use cases. Now, we’re going to talk about implementation. Since I’ve been working in JavaScript as of late, we’re going to use JavaScript to code it. Here. We. Go.

Implementation of the base classes

There are two main classes for the Binary search tree, and that’s the Tree class and the node class, similar to the linked list class.

Tree class:

class BinarySearchTree{
     constructor(){
          this.root = null
     }
}

Node class:

class Node{
     constructor(value){
          this.value = value;
          this.left = null;
          this.right = null
     }
}

The tree class itself is pretty simple. It just has a root value that points to the root node (recall the upside-down tree). Nodes are a little bit heftier. Not only does it have a value property, but also properties that point to its children.

Insertion and Searching

Let’s take the following BST as an example:

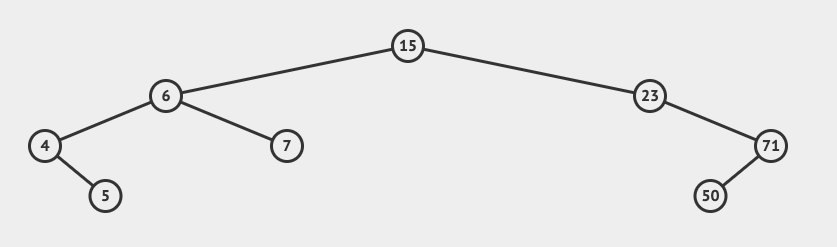
Notice that our root is 15. Recall that everything left of a node has a value less than it’s parent, and everything on the right has a value larger than its parent. With this in mind, we can think through an insertion method. Let’s say we want to insert the value of 9 into this tree. First, first, the tree will check it against its root, 15. Since the value to be inserted is less than 15, well go left. Next, we’ll check it against 6, and go right. Finally, we check it against 7 and go right. Since we have nowhere else to go, we found our insertion point. The gif below demonstrates this process.

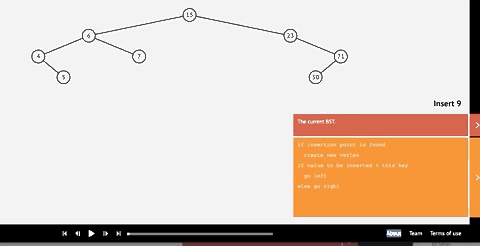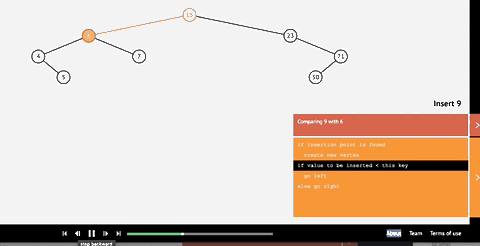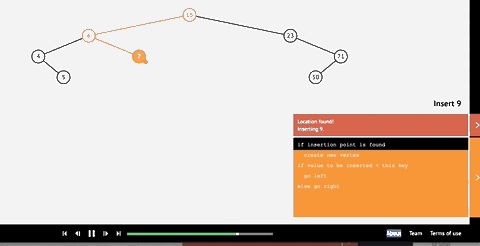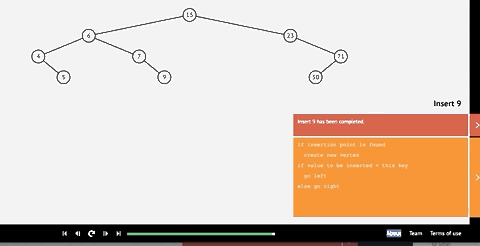
Insertion code

//snippet within BST class
insert(value){
     let newNode = new NodeValue(value)
     if(this.root === null){
          this.root = newNode;
          return this;
     }
     else {
          let current = this.root
          while(true){
               if(value === current.value) break; 
               //what you do if there's a value that exists already 
               //is entirely up to you
               if(value < current.value){
                    if(current.left === null){
                         current.left = newNode;
                         return this;
                    } 
                    else {
                         current = current.left
                    }
               }
               else if(value > current.value){
                    if(current.right === null){
                         current.right = newNode;
                         return this;
                    } 
                    else {
                         current = current.right
                    }
               }
          }
     }
}

Searching

For a BST, searching has relatively the same principals as inserting, but instead of inserting a node, we’re just checking for values. Since we’re using a BST, we’re assuming the tree structure has low values on the left, and high values on the right. We can use the same traversal logic for insertion for searching. If we reach the end of a branch but end up coming short, that means the node does not exist in the tree.

Searching Code

//snippet within BST class
search(value){
     if(this.root === null){
          return false
     }
     else {
          let current = this.root
          let found = false
          while(current && !found){
               if(value < current.value){
                    current = current.left
               }
               else if(value > current.value){
                    current = current.right
               }
               else{
                    return true
               }
          }
     }
     return false
}

So that’s searching and inserting in a Binary Search Tree.

BUT NICK. You may ask. What if the nodes are unordered. What then??

Well, I’m glad you asked! But first, we’re going to take a little detour….into RECURSION. Tune in next time!