
You know, you’d think I’d be taking a break on data structures and talk about other things like JavaScript, Ruby or anything less computer science-esque related.

I was going down that road too, but after encountering the topic of trees on a recent code challenge, I took it as an opportunity to learn about the ins and outs of it for next time I encounter it.
So what exactly are trees?
Trees are a little bit more complex than a linked list. Remember that linked lists are linear structures, with nodes pointing only to their immediate neighbor. The concept of nodes having a pointer that points to the next node gets carried over to binary trees, albeit a bit modified.
So to start off, a tree is a structure that consists of nodes in a parent/child relationship. So from one node, we can have it connect to another node or many nodes, be it 2 or 10 or whatever number. Each connection is then considered a “branch”, hence the name of tree. Try to visualize an actual tree:

Notice where the tree diverges and splits up. Visually speaking, those would be points where the nodes exist. Now for a more typical visual representation of a tree data structure:
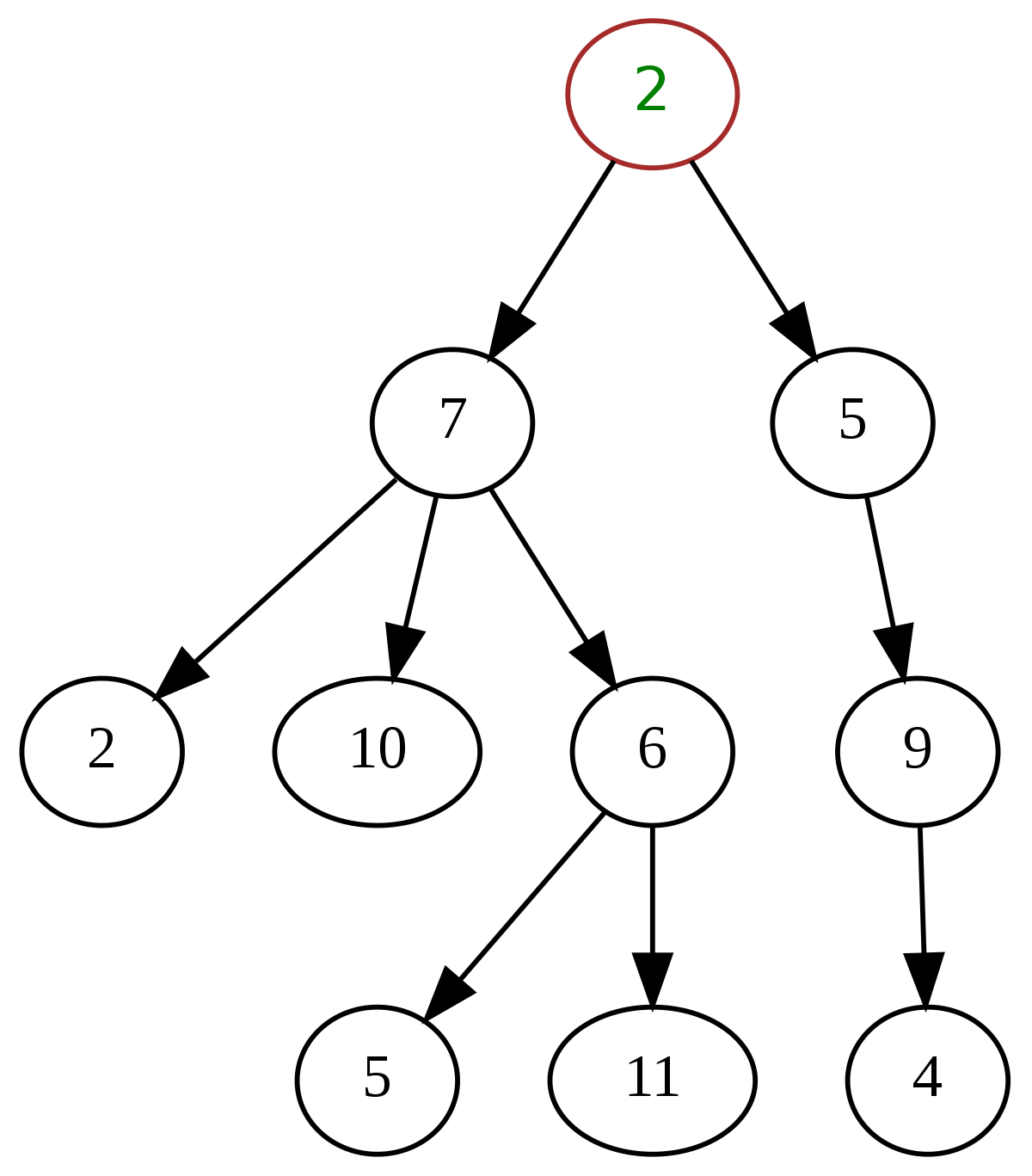
Think of it as a tree, flipped upside down. The ‘2’ at the top would be like the trunk, or “root”. Its children would be the nodes that consist of ‘7’ and ‘5’. The ‘2’ node object would have pointers to those children, so think of those pointers as the ‘branches’. As you go down, the ‘7’ and ‘5’ nodes start to branch off and have their own respective children. Finally, it’s possible that those children have their own children. And so we go. Unlike linked lists, there can be multiple paths to an endpoint.
Some other details:
- Child nodes can’t point to parent nodes.
- Child nodes with the same parent are referred to as ‘siblings’. Remember the child/parent relationship analogy? In a tree, sibling nodes can’t point to each other. That would make the tree into a graph, which I’ll write about someday in the future.
- Nodes with no children are referred to as leaves.
- The proper terminology for a connection between one node and another is ‘edge’.

Keep in mind that in a lot of examples, you’ll see numbers stored in these nodes, but the value of the node can pretty much be anything.
Use cases
Trees are used all the time, whether we realize it or not. A common example used is the HTML Document Object Model, or DOM. If you know your HTML web page structure, a web page starts at the HTML root, and then it’s children could be tags like head or body. From the body tag comes a slew of children, like the p tags, ul tags, divs, etc.
File systems can also be thought of as a tree. If you use a windows machine, you can think of the C:/ drive as the root and its folders as its children. Each folder could have its own files and subdirectories.
If you’ve played old point and click adventures, like “Secret of Monkey Island”, or even modern games like “Mass Effect”, you could affect various parts of the plot and your character progression through decision trees. You do one action, result A happens. Do another, and result B could happen. Although it’s not apparent, trees are everywhere.
So. Binary trees.
Right! There are many tree types out there with their own little unique features. If you know your Latin, ‘bi’ means two. So in a binary tree, nodes can have up to two children. So, no children, one child, or two children. No more than that.
And a binary search tree?
It’s a special version of the binary tree that is kept in a specific order. BST’s have data that can be compared, be it strings or numbers or whatever can be comparable. For each node, all data that are less than the node is left of the node, and all data larger than the node is on the right side. You can repeat it for each child node.

Let’s say in the example above in the root node of ‘8’, all child nodes left of ‘8’ have values less than 8, while all values right of ‘8’ have values greater than 8. As we go down the tree, taking ‘3’ as an example, all nodes left of ‘3’ have values less than 3, while all values greater than ‘3’ are on the right side, while at the same time still being less than 8 since it’s still on the left of 8.
To sum up, in a BST, all data is organized in a particular order.
Next time.
We’re going to talk about implementation. See you next time!